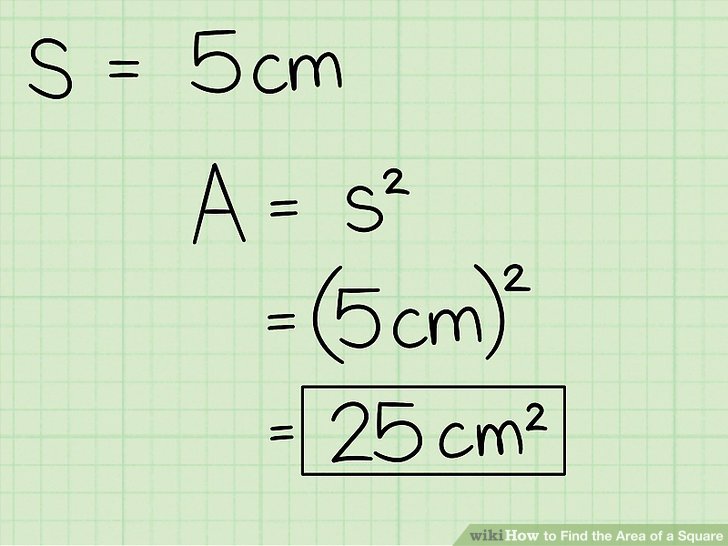Kaip Apskaičiuoti Kvadrato Plotą?

Kvadrato plotą lengva rasti, jei žinote jo kraštinės, perimetro ar įstrižainės ilgį.

Kvadrato ploto radimas naudojant kraštinės ilgį:

• Tarkime, kad kraštinės (S) ilgis yra 3 cm.

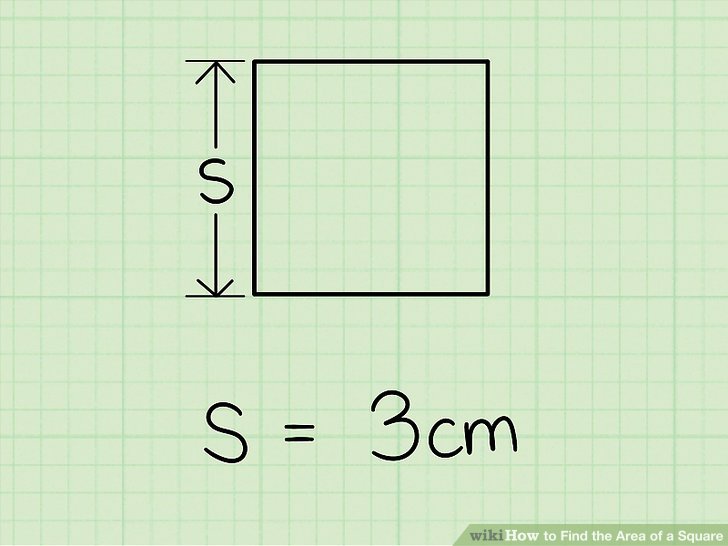
• Kvadrato ploto (A) formulė: A = SxS cm². 
• Kadangi visi kvadratai turi vienodo ilgio kraštines, galite tiesiog padauginti jų ilgį. 
• Jei kvadrato kraštinės ilgis yra 3 centimetrai, tada jūs tiesiog turite kvadratu pakelti skaičių 3, kad surastumėte kvadrato plotą: A = 3² = 9 cm².

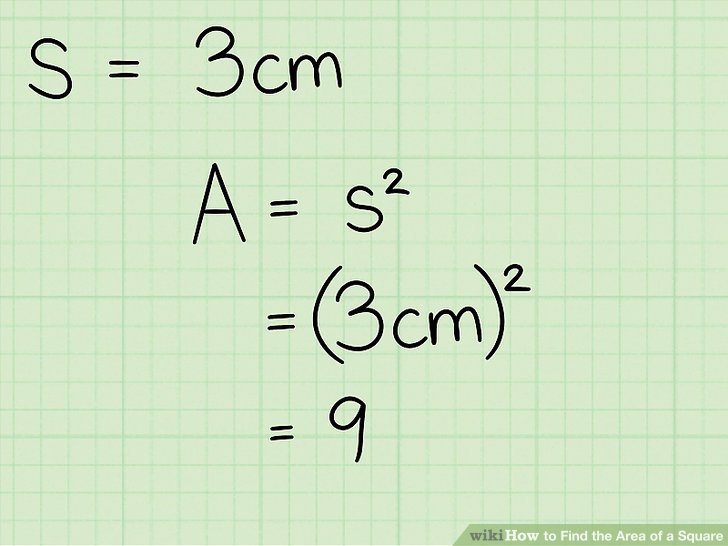
• Atsakymą būtinai nurodykite kvadratiniais vienetais.
• Kvadrato kraštinės kvadratas yra tas pats, kas kvadrato aukštį padauginti iš jo pagrindo ir taip surandamas kvadrato plotas.

Kvadrato ploto radimas naudojant žinomą įstrižainę:

• Tarkime, kad kvadrato įstrižainės (d) ilgis yra 5 cm.

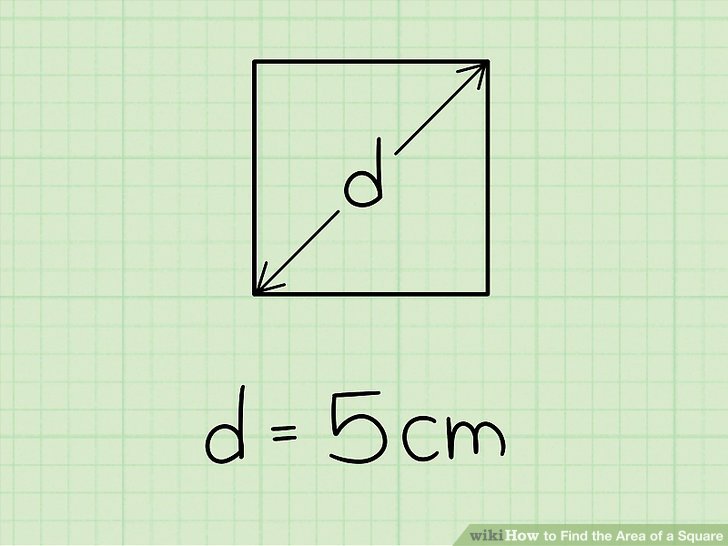
• Kvadrato ploto (A) formulė žinant įstrižainę yra: A = d²/2 cm².

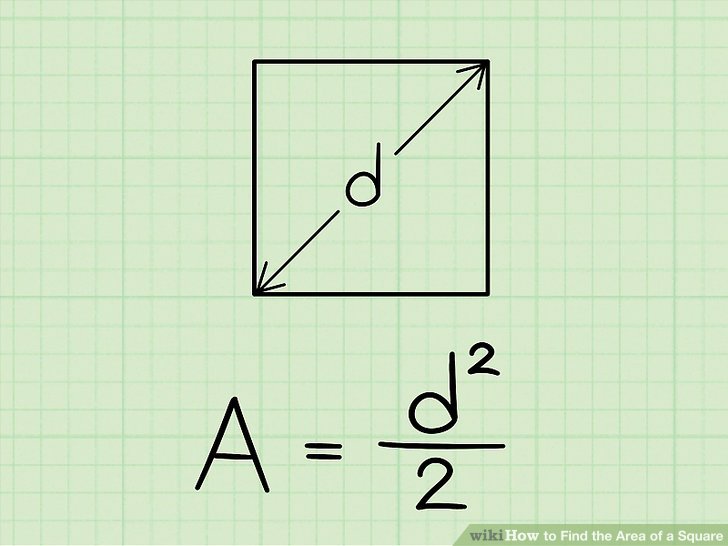
• Taigi, jūs turite žinomos įstrižainės ilgį pakelti kvadratu: 5² cm.

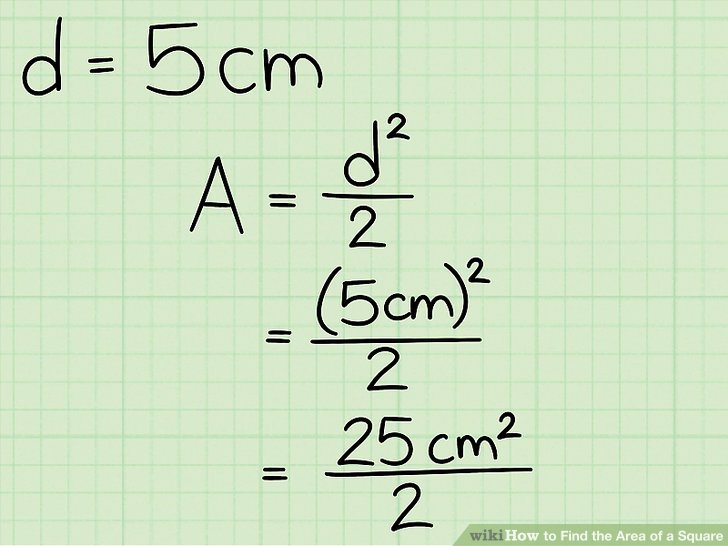
• Tada gautą skaičių padalinkite iš 2: 25 cm²/ 2, o tai yra lygu 12,5 cm². 
• Taigi, skaičiavimą užrašome taip: A = 5² / 2 = 25 / 2 = 12,5 cm².

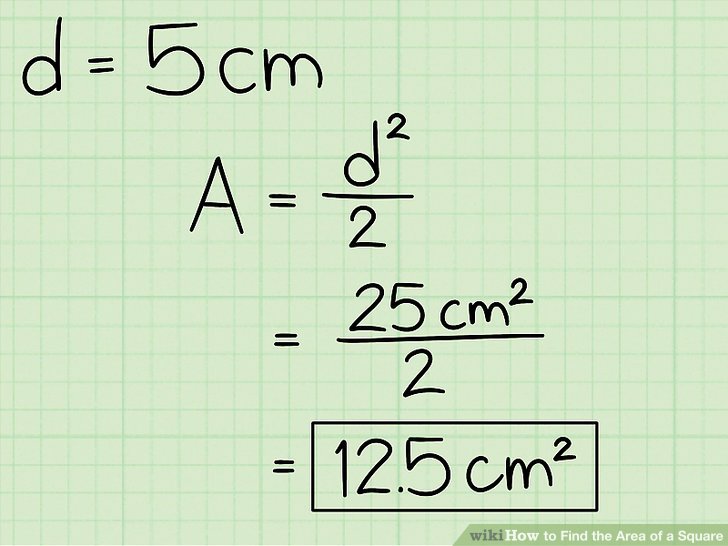
Kvadrato ploto radimas naudojant žinomą perimetrą:

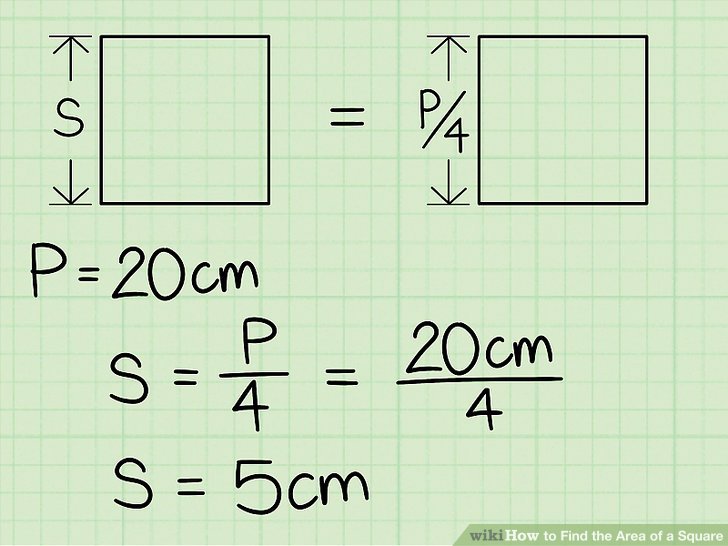
• Padauginkite perimetrą (P) iš 1/4, kad rastumėte kraštinės ilgį. 
• Tai tas pats, kas perimetrą padalyti iš 4, nes kvadratą sudaro keturios kraštinės (S) ir kiekviena kraštinė yra vienodo ilgio.
• Tarkime, kvadrato perimetras yra 20 cm, tada tiesiog padauginkite 20 cm iš 1/4: S = 20 cm x 1/4 = 5 cm. 
• Jūs žinote, kad kvadrato kraštinės ilgis yra 5 centimetrai.

• Dabar, kai žinote, kad kraštinės ilgis yra 5 centimetrai, galite naudoti šią formulę: A = S²cm².
• A = (5 cm)² = 25 cm².