Kaip Apskaičiuoti Trikampio Plotą?

Populiariausias būdas apskaičiuoti trikampio plotą yra pasinaudoti trikampio pagrindu ir aukštine. Egzistuoja daugybė įvairių formulių, kaip rasti trikampio plotą, tačiau visada reikia atsižvelgti į tai, kokie duomenys turimi. Pavyzdžiui, trikampio plotą galima apskaičiuoti ir žinant trikampio šonines kraštines ar kampus.

Trikampio Plotas Pagal Aukštinę

1. Raskite trikampio pagrindą (b) ir aukštinę (h). Pagrindu laikoma viena trikampio pusė (kraštinė), o aukštine – statmuo, išvestas iš trikampio viršūnės į tiesę. Jis randamas padalijant trikampį į dvi lygias dalis, iš trikampio viršūnės nubrėžiant tiesę, statmeną trikampio pagrindui. Jūs turite žinoti šiuos duomenis arba mokėti išmatuoti trikampio kraštinės ilgį.

Pavyzdys. Trikampio pagrindo ilgis – yra 5 cm, o aukštis – 3 cm.

2. Pasinaudokite trikampio ploto formule:

kur S yra plotas, b – trikampio pagrindo ilgis, h – trikampio aukštinė.

3. Įtraukite pagrindą ir aukštinę į ploto formulę. Padauginkite abi reikšmes, gautą sandaugą padauginkite iš . Išsiaiškinsite trikampio plotą kvadratiniais centimetrais.

Pavyzdys. Trikampio plotą, kurio pagrindo ilgis yra 5 cm, o aukštis – 3 cm, apskaičiuoti reikėtų taip:

Taigi, trikampio, kurio pagrindas ilgis yra 5 cm, o aukštis – 3 cm, plotas yra 7,5 cm².

Apskaičiuokite stačiojo trikampio plotą. Kadangi dvi stačiojo trikampio kraštinės yra statmenos, viena iš statmenų kraštinių bus trikampio aukštinė, o kita – pagrindas. Jei aukštinė ir (arba) pagrindas nenurodytas, juos nesunku apskaičiuoti žinant šoninių trikampio kraštinių ilgius. Galite pasinaudoti šia formule:

• Galite naudoti šią formulę, jeigu žinote vienos kraštinės ilgį ir įžambinę. Įžambinė – stačiojo trikampio kraštinė, esanti prieš statųjį kampą. Atminkite, kad surasti nežinomos kraštinės ilgį (įžambinę) galima panaudojant Pitagoro teoremą: a² + b² = c².

Pavyzdys. Jei trikampio įžambinė yra šoninė kraštinė c, aukštinė ir pagrindas – a ir b. Jei žinote, kad įžambinė yra 5 cm, o pagrindas – 4 cm, tai pasinaudokite Pitagoro teorema, kad surastumėte kraštinės aukštį:

Įterpkite statmenų trikampio kraštinių ilgius (a ir b) į trikampio ploto formulę.

Trikampio Plotas Pagal Kraštines

1. Apskaičiuokite trikampio pusperimetrį. Trikampio pusperimetris lygus pusei figūros perimetro. Norėdami rasti pusperimetrį, pirmiausia apskaičiuokite trikampio perimetrą, sudėję trijų jo kraštinių ilgius. Tada padauginkite iš .

Pavyzdys. Jei yra žinomos visos trys trikampio kraštinės – 5 cm, 4 cm ir 3 cm – tai pusperimetrį galima sužinoti taikant formulę:

2. Pritaikykite Herono formulę: , kur a, b, c – kraštinės, o p – pusperimetris.
3. Pusperimetrį ir šoninių kraštinių ilgį įtraukite į formulę.

Pavyzdys:

4. Apskaičiuokite skliaustuose esančias reikšmes. Iš pusperimetrio atimkite kiekvienos kraštinės ilgį. Tada padauginkite šias reikšmes.

Pavyzdys:

5. Padauginkite dvi gautas reikšmes. Tada ištraukite jų kvadratinę šaknį, sužinosite trikampio plotą kvadratiniais centimetrais.

Taigi, trikampio plotas – 6 cm².

Lygiakraščio Trikampio Plotas

1. Raskite vienos trikampio kraštinės ilgį. Visų lygiakraščio trikampio kraštinių ilgis yra vienodas, tad žinodami vienos kraštinės ilgį, žinosite visų trijų kraštinių ilgį.

Pavyzdys. Kiekviena trikampio kraštinė – 6 cm.

2. Pritaikykite formulę lygiakraščio trikampio plotui apskaičiuoti: , kur a – vienos trikampio kraštinės ilgis.
3. Įtraukite šoninės trikampio kraštinės ilgį į formulę. Kraštinių reikšmę pakelkite kvadratu.

Pavyzdys. Lygiakraščio trikampio kraštinės ilgis – 6 cm.

4. Iš kvadrato ištraukite šaknį . Tai geriausia daryti skaičiuotuvu, kad gautumėte kuo tikslesnį atsakymą. Kitu atveju, šaknies reikšmei suapvalinti galima naudoti 1,732.

Pavyzdys:

5. Gautą reikšmę padalinkite iš 4. Sužinosite trikampio plotą kvadratiniais centimetrais.

Taigi, lygiakraščio trikampio, kurio kraštinės ilgis yra 6 cm ilgio, plotas yra apie 15,59 cm².

Trigonometrija

1. Raskite dviejų gretimų šoninių kraštinių ilgius ir kampą. Gretimos kraštinės yra dvi trikampio kraštinės, kurios susikerta figūros viršūnėje. O kampas – tai kampas, esantis tarp tų dviejų kraštinių.

Pavyzdys. Lygiakraštis trikampis, kurio dviejų gretimų kraštinių ilgis – 150 cm ir 231 cm, o kampas tarp jų yra 123 laipsniai.

2. Pasinaudokite trigonometrijos formule trikampio plotui apskaičiuoti: , kur b ir c – gretimosios kraštinės, o A – kampas tarp jų.
3. Įtraukite šoninių kraštinių ilgius į formulę. Būtinai pakeiskite kintamuosius b ir c. Padauginkite jų reikšmes ir gautą sandaugą padalykite iš 2.
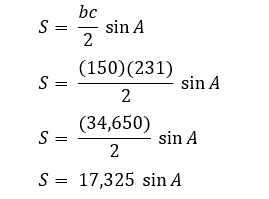
4. Į formulę įtraukite kampo sinusą. Sinusą galite rasti pasinaudodami skaičiuokle, įvesdami kampo reikšmę ir paspausdami mygtuką „SIN“.

123 laipsnių kampo sinusas yra .83867, taigi formulė bus:

5. Sudauginkite gautas reikšmes. Žinosite trikampio plotą kvadratiniais centimetrais.

Pavyzdys:

Taigi, trikampio plotas yra apie 14 530 cm².

D.U.K.

1. Kaip apskaičiuoti trikampio plotą?

Pasinaudokite trikampio kraštinių ilgiu ir aukštine, t. y. statmeniu, išvestu iš trikampio viršūnės į tiesę.

2. Kaip rasti trikampio perimetrą ir plotą?

Trikampio perimetrą apskaičiuosite susumavę visų 3 trikampio kraštinių ilgius. Norėdami apskaičiuoti trikampio plotą, padauginkite pagrindą iš aukštinės ir gautą reikšmę padalykite iš 2.

3. Kaip apskaičiuoti trikampio plotą?

Trikampio plotą galite rasti padauginę pagrindą iš aukštinės ir gautą reikšmę padalinę iš 2. Pavyzdžiui, jei turite trikampį, kurio pagrindas yra 4 cm, o aukštinė – 2 cm, tuomet trikampio plotas yra 4 cm², nes 4 x 2 = 8, o 8 / 2 = 4.

4. Kaip rasti trikampio ilgį ir plotį prieš apskaičiuojant plotą?

Tai sudėtingesnis procesas. Jei tai statusis trikampis, naudokite Pitagoro teoremą (a² + b² = c²), kad surastumėte trūkstamą trikampio kraštinę.

5. Kaip apskaičiuoti lygiakraščio trikampio plotą?

Jei žinote trikampio pagrindo ilgį ir aukštinę, galite naudoti standartinę formulę S = 1 / 2bh. Jei žinote trikampio kraštinių ilgius, galite naudoti šiame straipsnyje aprašytą lygiakraščių trikampių ploto apskaičiavimo metodą.

6. Kaip apskaičiuoti lygiašonio stačiojo trikampio plotą?

Kraštinės turi būti lygios, todėl kraštinės ilgį pakelkite kvadratu ir gautą reikšmę padalykite iš 2.

7. Kaip apskaičiuoti lygiakraščio trikampio plotą, jei nežinomi kraštinių ilgiai?

Tai susiję su trigonometrija. Turite rasti trikampio aukštinę – statmenį, išvestą iš trikampio viršūnės į tiesę. Aukštinė apskaičiuojama padauginus šoninės trikampio kraštinės ilgį (x) iš pusės 60 ° tangento (60 ° – visi lygiakraščio trikampio kampai). Gauta reikšmė turi būti lygi 0,866. Taigi aukštinė (0,866x) turi būti padauginta iš x ir padalyta iš dviejų, kad būtų gautas plotą.

8. Trikampio plotas yra 24 cm², aukštinė – 6 cm. Koks trikampio pagrindo ilgis?

Trikampio pagrindas apskaičiuojamas trikampio plotą pakėlus kvadratu ir padalijus iš aukštinės.

9. Trikampio pagrindo ilgis yra 2x + 4, o aukštinė – 3y. Koks trikampio plotas?

Neturėdami daugiau duomenų, negausite tikslios reikšmės. Tačiau galite nurodyti aukštinę kaip 1 / 2bh reikšmę, pridėdami pagrindo ir aukštinės reikšmes. Taigi plotas yra 1/2 (2x + 4) (3y); (x + 2) (3y); 3xy + 6y.

10. Kaip apskaičiuoti trikampio aukštinę, jei žinomas jo plotas ir pagrindo ilgis?

Pakelkite plotą kvadratu ir padalykite iš pagrindo ilgio.